Рис. 1. Возрастные пирамиды женских стабильных населений при различных коэффициентах естественного прироста r (o/oo) и одной и той же функции дожития.
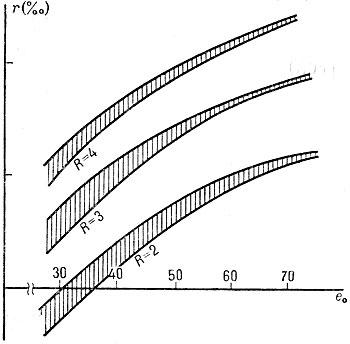
При одной и той же функции дожития l(х) положит. значениям r соответствует более молодая возрастная структура С. н. и с ростом r состав нас. омолаживается (см. рис. 1). В табл. 1 приведены основные характеристики структуры С. н. при разл. коэфф. естеств. прироста r и функциях дожития, соответствующих типовым таблицам смертности ООН со значением ср. продолжительности жизни при рождении для обоих полов вместе e0 = 20, 40, 60, 70 лет.
так что доля лиц в интервале возрастов x1x2 равна
Возрастная структура С. н. описывается функцией с(х):
Числ. С. н. в момент t равна:
где lF(x) - функция дожития для жен. нас., fF(x) - функция жен. рождаемости, т. е. вероятность рождения девочки у женщины в интервале возрастов x, x+Δx равна fF(x) Δx.
Между осн. количеств, характеристиками С. н. существует тесная связь. Для определения всех параметров С. н. достаточно задать функцию рождаемости f(x) и функцию дожития l(х). Коэфф. естеств. прироста С. н. представляет собой единственный действит. корень уравнения
Существуют непрерывные и дискретные модели С. н. В основе непрерывных лежит интегральное уравнение воспроиз-ва нас., в основе дискретных - матричная модель (см. Модели воспроизводства населения). Модель С. н., как правило, описывает нас. к.-л. одного пола, гл. обр. женское.
Табл. 1. - Возрастно-половая структура стабильного населения с различными функциями дожития и коэффициентом естественного прироста, o/oo
Модель С. н. применяется, во-первых, как основа для расчёта интегральных характеристик режима воспроиз-ва нас., таких, как истинный коэффициент естеств. прироста, истинные коэфф. рождаемости и смертности. Во-вторых, она используется для анализа взаимного влияния режима рождаемости и порядка вымирания, с одной стороны, и возрастной структуры нас.- с другой. В-греть-их, применяется в демографич. расчётах и прогнозах при отсутствии достоверных статистич. данных о нас. (применительно к нас. с относительно неизменным режимом воспроиз-ва). В-четвёртых, используется как составная часть др. демографич. и экон. моделей.
Никакое реальное нас. не является в точном смысле С. н., однако для любого нас. известны длит. временные интервалы, в течение к-рых режим рождаемости и порядок вымирания, подвергаясь тем или иным периодич. или случайным колебаниям, в среднем оставались практически неизменными. Воспроиз-во нас. в этом случае может быть с достаточной точностью описано с помощью модели С. н.
С. н. является упрощённым изображением реальных взаимосвязей демографич. процессов и возрастной структуры нас. Теория С. н. позволяет анализировать закономерности воспроиз-ва нас. при разл. гипотезах естеств. прироста населения.
Это свойство наз. сильной эргодичности свойством, а нас. - асимптотически С. н.
СТАБИЛЬНОЕ НАСЕЛЕНИЕ (от лат. stabilis - постоянный, неизменный, устойчивый), теоретич. модель нас. с неизменными во времени возрастными интенсивностями рождаемости, смертности и возрастной структурой населения. С. н. предполагается закрытым, т. е. не подверженным миграц. процессам. Применение модели С. н. в демографич. анализе основано на трёх свойствах: 1) С. н. обладает неизменным во времени коэффициентом естественного прироста населения; следовательно, изменение его числ. описывается экспоненциальной функцией времени, а С. н. - частный случай экспоненциального населения. 2) Каждому сочетанию режима рождаемости и порядка вымирания соответствует единственное С. н., с одному ему присущими характеристиками режима воспроизводства населения. 3) У нас., в к-ром с нек-рого момента времени остаются неизменными режим рождаемости и порядок вымирания, постепенно стабилизируется и возрастная структура.
Расстановка ударений: СТАБИ`ЛЬНОЕ НАСЕЛЕ`НИЕ
СТАБИЛЬНОЕ НАСЕЛЕНИЕ
Цифровые библиотеки и аудиокниги на дисках почтой от INNOBI.RU
. Для мужчин сотни.
Пользовательского поиска
СТАБИЛЬНОЕ НАСЕЛЕНИЕ
Комментариев нет:
Отправить комментарий